Introdução a Análise de Redes de Colaboração

A Análise de Redes de Colaboração (ARC) é uma abordagem metodológica, originada das ciências sociais, que utiliza os conceitos da teoria de grafos para descrever, entender e explicar as estruturas sociais e os relacionamentos entre os membros de uma rede (WASSERMAN e FAUST, 1994).

Além disso, a ARC permite observar as relações que facilitam ou dificultam as redes de colaboração e o compartilhamento de informação e conhecimento em uma organização. As observações oriundas da ARC podem indicar gargalos ou oportunidades para a melhoria do fluxo de processos, para evitar problemas de comunicação e perda de informações e conhecimento que deveriam circular na rede. Após diagnosticar os possíveis problemas, é possível propor algumas sugestões de melhorias para ajudar a organização a alcançar uma colaboração e comunicação efetivas (CROSS et al., 2004, MONCLAR et al., 2011).

Metodologia para Estudo de Redes de Colaboração

A metodologia para estudo de redes de colaboração é composta por quatro passos (CROSS et al., 2004):

(i) definição da rede que se deseja analisar: O primeiro passo é definir o objetivo da análise e estabelecer a semântica dos nós e arestas da rede que se deseja analisar. Além disso, a análise da rede será potencialmente mais benéfica em redes que tenham uma maior necessidade ou potencial de colaboração e aonde a colaboração seja importante para a organização e traga benefícios estratégicos ou operacionais;

(ii) coleta dos dados necessários: O próximo passo é a coleta de dados para a construção da rede de colaboração. Esta coleta pode ser feita através de questionários (papel, e-mail ou Internet) ou facilitada pela mineração de dados (AALST et al., 2005) que busca os dados em repositórios de informação para que eles possam ser manipulados para visualização ou análise;

(iii) visualização de redes: representação visual das informações, através de diferentes formas, para diminuir a sobrecarga cognitiva do usuário e facilitar a compreensão e exploração dos dados através de imagens (VIEGAS e DONATH, 2004). Além disso, a visualização aproveita a habilidade do ser humano no reconhecimento de padrões e estruturas em informações visuais. Portanto, torna mais fácil e natural a tarefa de compreensão das informações apresentadas. No entanto, a visualização também possui limitações no caso de diagramas de grande dimensão, devido à sobreposição de elementos.


A visualização de redes de colaboração permite a observação de fatos e a extração de conhecimento a partir de grafos (FREITAS et al., 2008). Além disso, a visualização de uma rede é útil para identificar pessoas chave, para a compreensão da estrutura de formação ou para comparar redes semelhantes. Tamanho, forma ou cor podem ser usados para codificar informações em um nó ou aresta, aumentando o poder expressivo da visualização.

Por outro lado, os mecanismos de visualização se diferenciam pelos recursos que oferecem e pelas perspectivas que exploram. Na perspectiva temporal, por exemplo, o interesse gira em torno do entendimento da dinamicidade da rede, ou seja, como as redes se desenvolvem ou mudam no decorrer do tempo.

Leia também:

A visualização da rede é uma informação importante, pois oferece percepção sobre o que está acontecendo com as interações ou colaboração do grupo. Entretanto, sozinha, a visualização não permite a total compreensão da colaboração existente entre os atores da rede e precisa ser complementada pela análise das redes, que é o passo seguinte da metodologia.

(iv) análise de redes: Por fim, o passo de análise de redes de colaboração utiliza, portanto, as propriedades topológicas oriundas da teoria de grafos para descrever a interação e a organização social de um grupo. O objetivo é entender padrões, geralmente implícitos, nos relacionamentos existentes entre os nós de uma rede. Além disso, é considerada como um “raio-x da organização”, e pode ser usada como uma ferramenta de diagnóstico e planejamento para aumentar a colaboração e, consequentemente, o fluxo de informações e processos na organização.

Propriedades de análise de redes de colaboração

As redes de colaboração podem ser analisadas através das suas propriedades (WASSERMAN e FAUST, 1994). Assim, um dos principais usos da ARC é medir a importância de um nó dentro da rede. Além disso, um nó da rede é considerado proeminente se os seus relacionamentos o tornam particularmente visível aos outros nós da rede. Dessa forma, existem duas classes de proeminência do ator: centralidade e prestígio (WASSERMAN e FAUST, 1994).

Na centralidade, a direção das relações nas quais o ator está envolvido não importa, ou seja, um nó central é aquele que está intensivamente envolvido em relacionamentos com outros atores, seja como transmissor ou como receptor. Por sua vez, o conceito de prestígio do ator é mais restritivo, pois só reconhece as relações onde o ator é o receptor. Assim, o conceito de prestígio do ator não pode ser observado em um grafo não direcionado.

Entre os tipos de centralidade (FREEMAN, 1978, WASSERMAN e FAUST, 1994), destacam-se:

Centralidade de grau (degree centrality):

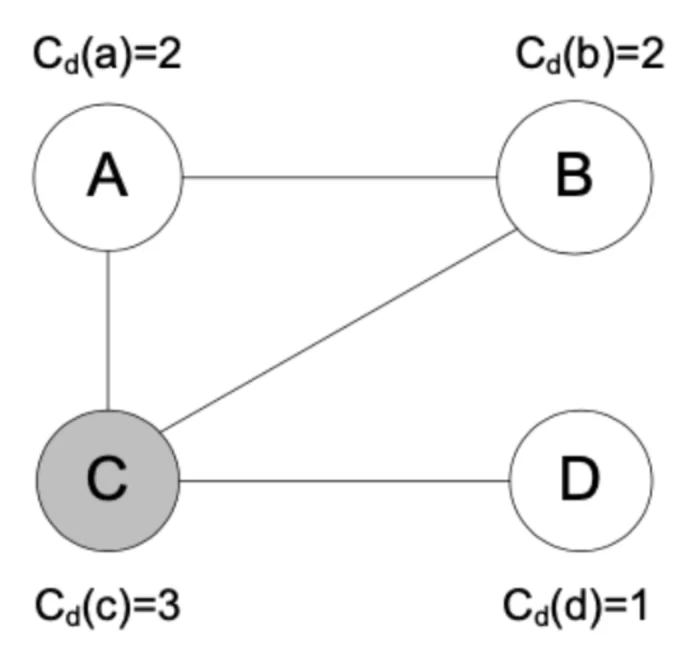
Está relacionada ao número de relações diretas que este nó mantém na rede. O nó mais central ou hub (BARABASI, 2003) é aquele que possui o maior grau. Como ele está em contato direto com muitos outros nós, ele acaba ocupando um lugar central na rede e desempenhando um papel importante. Em contrapartida, nós com grau pequeno ocupam uma posição periférica na rede. Usando o grafo apresentado na figura abaixo como exemplo, o nó mais central é o nó c que possui a maior centralidade de grau, que é igual a 3, pois possui 3 arestas. Os outros nós não atingem centralidade de grau igual a 3. Os nós a e b possuem centralidade de grau igual a 2 e o nó d possui a menor centralidade de grau desta rede que é igual a 1;

Exemplo de centralidade de grau
Centralidade de grau

Centralidade de proximidade (closeness centrality)

Identifica uma posição estratégica na rede e está inversamente relacionada com a distância. Ela representa o quão próximo um nó se encontra em relação aos demais nós da rede. Calculamos a centralidade de proximidade pelo inverso da soma das distâncias de um nó para os outros destinos possíveis. A ideia é que um nó é central se ele pode interagir rapidamente com os demais. Esse nó central pode ser altamente produtivo no compartilhamento de informações com o grupo, já que acelera o caminho de comunicação entre os nós.

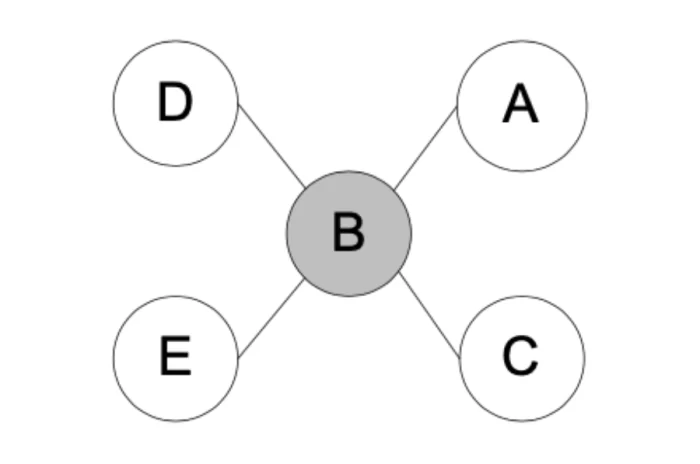
Assim, quanto menor a distância de um nó para o restante da rede, maior sua centralidade de proximidade. Em contraste, quanto maior a distância entre os nós, maior a chance de perda ou má interpretação entre as informações transferidas ao longo da rede. Considerando como exemplo a rede em formato de estrela apresentada na figura abaixo, o nó b, localizado no centro, é adjacente a todos os outros. Logo, ele tem uma centralidade de proximidade máxima, já que partindo de b todos os outros nós podem ser alcançados em apenas 1 passo.

Exemplo de centralidade de proximidade
Centralidade de proximidade

Centralidade de intermediação (betweenness centrality):

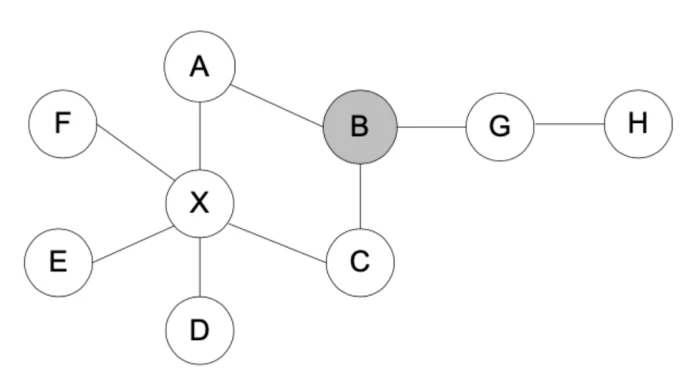
Os nós que se localizam no caminho entre dois nós não adjacentes influenciam as interações entre eles. Esses nós potencialmente controlam as interações entre os dois nós não adjacentes. Portanto, medimos a centralidade de intermediação pelo número de vezes que um nó aparece no menor caminho entre outros nós. Essa medida quantifica o grau em que um indivíduo na rede controla ou intermedia o fluxo de informação. Por exemplo, no grafo apresentado na figura abaixo, o nó b não possui a maior centralidade de grau, mas desempenha um papel importante na rede e tem uma alta centralidade de intermediação, pois atua como ponto de articulação entre os nós {a, c, d, e, f, x} e os nós {g, h};

Exemplo de centralidade de intermediação
Centralidade de intermediação

Apesar de essas propriedades de centralidade terem foco nos nós, elas também podem ser analisadas do ponto de vista da rede como um todo ou de determinados subgrupos. Desta forma, podem ser úteis para comparar diferentes redes, desde que sejam normalizadas de acordo com o tamanho da rede. Por outro lado, outras propriedades, como a densidade da rede, exploram diretamente as propriedades gerais da rede.

Densidade da rede:

A densidade de uma rede está relacionada à quantidade de arestas que mantêm interligado um conjunto de nós. Além disso, quanto mais arestas existirem em uma rede, mais densa ela será (WWF, 2003). Por conseguinte, a densidade indica a proporção entre o número de relacionamentos existentes e o número de relacionamentos possíveis. Desse modo, a densidade é uma propriedade importante para avaliar o nível de coesão existente na rede.

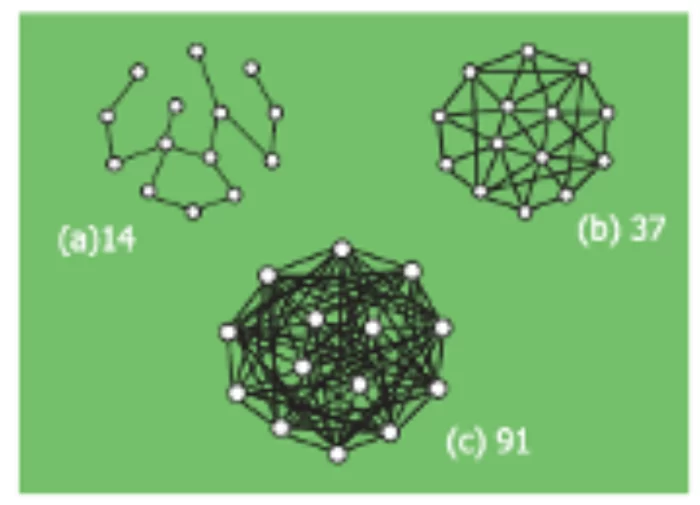
Por exemplo, na figura abaixo, a mesma rede, composta por 14 nós, é apresentada com número de arestas e, consequentemente, densidades diferentes. No diagrama (a), os nós estão interligados por apenas 14 arestas, o que resulta em uma densidade baixa de 0,15. No diagrama (b), 37 arestas relacionam os nós, representando uma densidade de 0,4. Por fim, no diagrama (c), os mesmos 14 nós ligam-se por meio de 91 arestas, onde a densidade resultante é máxima e igual a 1, pois todos os nós estabelecem ligações com os demais formando um grafo completo.

Exemplo de densidade da rede
Densidade da rede (WWF, 2003)

Conclusão

Sabe-se que a colaboração tem um papel essencial para o sucesso dos negócios. Se você não entender as redes, sua dinâmica, sua formação, como irá fomentá-las? As redes ajudam na compreensão de determinados fenômenos e suas conexões. Assim, podem ser utilizadas para explicitar e acompanhar a colaboração existente entre os participantes de um processo ou entre diferentes organizações parceiras em um processo interorganizacional.

A ARC já foi explorada em diferentes contextos (MONCLAR et al., 2011): sociais (EGLER, 2007); ambientais (WWF, 2003); organizacionais (CROSS et al., 2004); de pesquisa científica (BIRD et al., 2009); melhorias de processos de software (NIELSEN e TJØRNEHØJ, 2005); na área de BPM como parte de uma estratégia de Social BPM (SWENSON et al., 2011); na área de CSCW (Computer Support Cooperative Work) para derivar requisitos para sistemas colaborativos (PEREIRA e SOARES, 2007); e no contexto do desenvolvimento de software.

Deve-se também observar que, além de aplicável em diferentes contextos, a ARC pode ser adotada para explorar as redes sociais sob os quatro aspectos de apoio à colaboração: comunicação (DAMIAN et al., 2010, PINZGER e GALL, 2010), coordenação (SANTOS et al., 2011), memória e percepção (DAMIAN et al., 2010, DE SOUZA e REDMILES, 2011).

Pensando nisso, a solução de colaboração da dheka leva em consideração a forma como os participantes (ou nós da rede) interagem e se relacionam assim como as especificidades relativas a cada contexto.

Referências